問題6-1(総当たり)
-

- 今回はじめて
-

- 5分
- 制限時間
- 1 : 30


問題

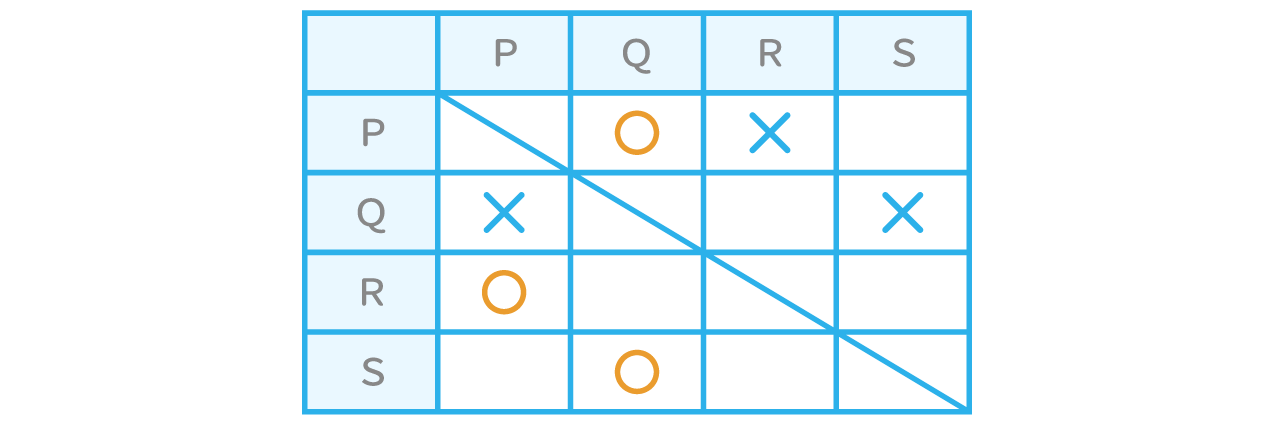
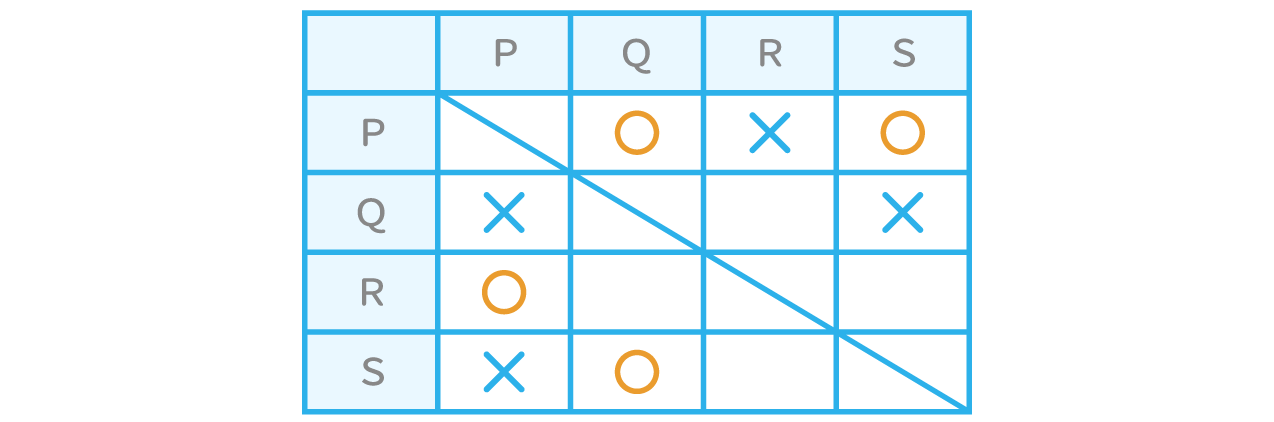
P、Q、R、Sの4チームが、バスケットボールの試合を総当たり戦で行った。その試合結果について、次のことが分かっている。
- ⅰ)Pは2勝1敗だった
- ⅱ)PはQに勝った
- ⅲ)RはPに勝った
- ⅳ)SはQに勝った
- ⅴ)引き分けの試合は無かった
- (1)次のア、イ、ウの推論のうち、必ずしも誤りとはいえない推論はどれか。
- アQは1勝2敗だった
- イRは全勝だった
- ウSは全勝だった
▼ 選択肢をクリックすると、採点して解答を表示します。


| Aアだけ |
| Bイだけ |
| Cウだけ |
| Dアとイの両方 |
| Eアとウの両方 |
| Fイとウの両方 |
| Gアとイとウのすべて |
| H必ずしも誤りとは言えない推論はない |
-

- 今回はじめて
-

- 5分
「最適学習モード」と「手書きメモツール」搭載、超効率的SPIスマホアプリを是非ご検討下さい!
90
5
4
D
30
10
0
2
110